Kursthemen
-
LECTURE N.1 sep 25 2023
Basic biology and computational biophysics, at the molecular level: The space of sequences as the archive of molecular evolution (Zuckerkandl&Pauling1965)
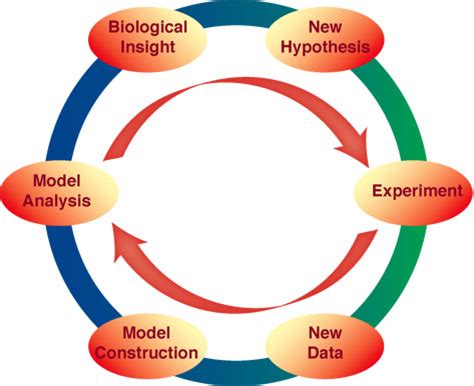
Models/Computation/Simulation
Deterministic/stochastic simulations (Bray2015)
Probabilities as conditional probabilities (van_de_Schoot2021)
Direct vs inverse problems
Biophysics in the XXI century: from molecular to integrative, evolutionary biophysics (an example:Terry Hwa): semantics: biological physics/physical biology; biologically inspired physics/biophysics
Physics of living systems vs physics of parts of living systems (Ageno’s [integrative] vs Careri’s [molecular] approaches)
Simplicity/complexity
Complex systems (layers and scales: “More is different”, Phil_Anderson1972) and living systems
Big data, the problem of “law without law” and the end of theory (readings: Wheeler1983, Caprara_Vulpiani2018)
The manifesto of the big data and artificial intelligence era (Chris_Anderson2008)
Top-down vs bottom-up approaches
(suggested general readings: Richard Holmes, The Age of Wonder: How the Romantic Generation Discovered the Beauty and Terror of Science (Published by HarperPress in 2008 ISBN 978-0-00-714952-0); Siri Hustvedt, “The Delusions of Certainty”, Simon & Schuster (ed. it. Le Illusioni della Certezza,Einaudi, 2018); Dennis Bray, “Wetware”, Yale University Press,2009 this is a rem book by one of the pioneers of systems biology)
(suggested general readings: Siri Hustvedt, “The Delusions of Certainty”, Simon & Schuster (ed. it. Le Illusioni della Certezza,
Einaudi, 2018); Dennis Bray, “Wetware”, Yale University Press,2009)
STUDY MATERIALS
slides CB_23_24_L1.pdf
further reference material in the CB_23_24_PACK_1
consider the text CB_23_24_Inaugural.pdf for a general discussion
-
FIND, HERE COLLECTED, THE STUDY MATERIALS AND SUGGESTED READINGS TO SET THE GENERAL STAGE OF THE COURSE
-
-
LECTURES N.2 AND 3, SEP 26 and 28 2023.
-Molecular structures and the Born-Oppenheimer approximation
-Basic principles of Ab-initio Molecular Dynamics: Born-Oppenheimer surfaces
-Hellman-Feynman TheoremMODELLING ε0(R) ---> FORCE FIELDS
Morse potential as the simplest force field
Force field as a network (just the concept)
Pairwise additive approximation
General form of a force field: bonded terms/non bonded terms
BIBLIOGRAPHY
Tuckerman_Born-Oppenheimer.pdf
Griebel2007_Numerical Simulation in Molecular Dynamics_Chap2.pdf [S]
Feynman1939,pdf [R] -
LECTURE N. 4 MON OCT 2 2023
Computation as an INPUT/OUTPUT process
Finite states machines
Effective procedures and computability of functions: algorithms
Non computability
Top-down / bottom-up methods
Study materials:
Chapter n.3 of Feynman’s lectures in Computation (1996)
See also, Computational models of science, chap 9 of Jean-Gui Meunier, Computational Semiotics (2021)
-
from Feynman's Lectures on Computation chap. 3
from Meunier's Computational Semiology chap.9
-
-
Lecture N. 5 TUE OCT 5 2023 room 8 12am-2pm
biological physics/physical biology; biologically inspired physics/biophysics
evolutionary distances (slides CB_22_23_L4.pdf, integrate with further self-study)
genomes and the genetic code: Central dogma of molecular biology, informational biomolecules: nucleic acids & proteins: peptide bonds formation and planarity, protein synthesis on the ribosome, genetic code and its degeneration (codon bias) (HA 2.2, 2.3)
what is darwinian evolution (HA 3.1,3.2, 3.3 (mutations), 3.4 (coalescence) 3.6 (neutral evolution and adaptation, codon bias))
the space of biological sequences as the archive of evolution (molecules as documents of evolutionary history, see: ZuckerkandlPauling1965
molecular evolution of nucleotide sequences
essential genes, homologous/paralogous genes
evolutionary distances d vs. sequence identity D
sequence/structure/dynamics/function
-
Find here materials to complement the track of this lectureN.4: In particular the introductory chapter of Weinberg's treatise on Cancer and the interesting paper Physics is life by Goldenfeld and Woese.
-
-
lectures N.6, 7, 8 and 9
Life is physics (Goldenberg-Woese)
What is evolution (HA 3.1), the naïve setting: mutation-selection (HA 3.2)
Species/speciation
The space of biological sequences as the archive of evolution (Molecules as documents of Evolutionary History (see: ZuckerkandlPauling1965)
Mutations (HA 3.2), sequence variation within and between species (HA 3.3)
Negative purifying vs positive Darwinian selectionEevolutionary pressure on a site through dn/ds [Ka/Ks] (optional) (HA 11.2.3)
Evolutionary distances between orthologous genes (HA 4.1.1)
Probabilistic models of evolution (DU chap 8.2)
The Jukes-Cantor model (HA 4.1.2 and Box 4.1)
Generative probabilistic models of sequence evolution: general scheme (HA 4.1)
Alphabets, symbols, states
Transition rates matrix
Dynamics between states: Master equations: in /out terms
Detailed balance
Alignments (genes/proteins)
Orthology paralogy, homology
The genetic code: codon bias
Why probabilistic evolutionary models?
substitution matrices (DU 2.2, Protein Substitutions Models (slides))
PAM model of protein sequence evolution (HA 4.2)
PAM distances (HA box 4.2)
Log-odd scoring PAM matrices (HA 4.3.1, DU chap 2)
BLOSUM scoring matrices (HA 4.3.3, DU chap.2)
STUDY MATERIALS IN CB_23_24_PACK_5
-
Slides and study materials
-
-
LECTURES: N, 10, 11, 12, 15 and 16
STUDY MATERIALS IN CB_23_24_PACXK_6PROTEINS BETWEEN ORDER AND DISORDER
Primary, secondary, tertiary and quaternary protein structures
Cellular Crowding, Chaperones, Co-translational folding/assembly
Standard form of the 20 naturally occurring amino acids: chirality of amino acids, formation of the peptide bond
Special amino acids: glycine, histydine, proline, cysteine (disulphide bridges)
Dihedral angles and Ramachandran plots: regions of standard secondary structures
Stabilizing forces in protein structure (electrostatic, van der Waals, hydrogen bonds, hydrophobic,…)
Water and protein conformations: role of hydrogen bonds
Principles of evolutionary protein design: positive/negative design
What is bioinformatics
Protein Data Bank (PDB): to visualize protein structures use Pymol, Chimera, Litemol on the .pdb files (see The language of the protein universe by M. Levitt)
free energy and the folding processstructural and functional protein domains (what is a protein domain? see also as a suggested reading: Pawson’s interaction domains, Pawson2002).
sequences determine protein structures (suggested reading: Anfinsen’s dogma, Anfinsen1973) and structures are more conserved than sequences
proteins: between order and disorder. CH plot (Uversky2002)
intrinsically disordered proteins (see databases: DISPROT, MobiDB)
Dihedral angles and Ramachandran plots: regions of standard secondary structures
Stabilizing forces in protein structure (electrostatic, van der Waals, hydrogen bonds, hydrophobic,…)
Water and protein conformations: role of hydrogen bonds
Principles of evolutionary protein design: positive/negative design
SUPERPOSING PROTEIN STRUCTURES
Structural distances and philogenetic distances
How to superpose protein structures in general (hard problem)
Subtract roto-translations + RMSD
Quaternions and rotations
-
Slides and study materials on PROTEINS
-
-
LECTURES N. 13, 14, 17 and 18
lecture 18 was devoted to the setup of a project on the comparison of the dynamical structure of native and mutated viral lysozymes
initial conditions, integration schemes, force fields, integration schemes, thermostats
biological energy scales/biological time scales/ timescales of protein motions
protein folding in vivo (crowding) / in vitro
free energy barriers control relaxation times
protein disorder/protein order in the simulation (solid-like vs liquid-like motions)
quantum mechanics vs Molecular Mechanics
force fields: bonded + nonbonded parametrisation (see also lecture N. 3)
energy minimisation and the protein folding problem (recent application of AI: ALPHA FOLD 2)
typical observables in a protein MD simulation: RMSD(t), RMSF(t), Rg(t)
structural superposition of proteins
the problem of roto-translation subtraction
symplectic integrators, Verlet's algorithm: remarks on the Liouville’s formulation of the discretized dynamics
(Tsai2004, Binder_Ciccotti1996.pdf, Schiller2008)
Trotter product formula of operators
CONTROLLING TEMPERATURE AND PRESSURE IN MD
MD as generator of thermodynamical statistics, overview
Liouville formulation of the MD, factorization
Ensembles
Constant temperature MD: quenches, Anderson Thermostat, Nosè-Hoover Thermostat
Temperature Echo
CB_23_24_PACK_7
-
Slides and supplemtary materials for the core lectures in MD of proteins
-
-
LECTURES N. 19 and 20
Introduction to Principal Components Analysis (PCA)
Dealing with multivariate contexts in which several correlated variables interfere in a phenomenon, the idea is to
LINEAR transform the original variables into uncorrelated ones that are ordered following their variance. The low variance transformed variables can be neglected, realizing a dimensional compression of the initial data.
Protein essential dynamics as PCA. The principal components associated to the multi-dimernsional protein dynamics are
collective coordinates of potential biological meaning.
STUDY MATERIALS IN CB-23_24_PACK_8
-
Slides and supplementary materials on PCA Essential Dynamics of proteins, collective coordinates
-
-
LECTURE N. 21 and 24 (extremely compressed, here and in the PACK find reference to materials that were mentioned)
simplicity/complexity/scales (Anderson1972)
micro/meso/macro scales: objects studied in diluted isolation (e.g. in vitro) and connected into a network of relationships (e.g. in vivo) , see Parisi's 2021 Nobel Lecture.
networks as a general model for complex systems.
structure meets networks at the nanoscale : Hi-C maps and the chromatin structure, see Kempfer_Pombo2019
elements of network models: nodes, links, adjacency matrices, degree distributions, power-laws (scale free-networks), communities [min-cut theorems]
Communities (Fortunato2016)
suggested general textbook: Vito Latora, Vincenzo Nicosia and Giovanni Russo, Complex Networks, Cambridge University Press 2016
(see in particular chapters 2 and 9)
inner networks in proteins structures and sequences (see Vendruscolo2002, Sladek2021, Estrada 2010)
Recurrence Quantification Analysis as an inner correlation/information network in physiological signals and proteins
(https://en.wikipedia.org/wiki/Recurrence_quantification_analysis)
protein-protein networks, interactomes (see STRING database (https://string-db.org/))
interactomes as information networks (see cancelled CENTURI 2021 Cargese meeting: https://centuri-livingsystems.org/csm2021/)
STUDY MATERIALS IN CB_23_24_PACK_9-
Find here suggested materials for further study
-
-
LECTURES N. 22 and 23
GUEST LECTURER Dr. Andrea Cappannini from the LABORATORY OF BIOINFORMATICS AND PROTEIN ENGINEERING (https://genesilico.pl) WARSAW PL
In the attached file you will find a list of the topics that have been discussed and an updated bibliography
-
LECTURES N.25 and 26 and 27
clustering (HA, 2.6 hierarchical vs partitioning methods, see also Altman2017).
distances, metric spaces
density based (topological) vs coupling (interaction) based methods
k-means, Dbscan, superparamagnetic (Domany2003)
information based methods (Bialek2004, Slonim2005, Luksza2010)
comparing clusterings: the mutual information approach (Meila2007, Vinh2010)
Partitioning clusterings as random fragmentation processes: breaking of self-averaging
(see: Andrea De Martino, The Geometrically Broken Object, 1998 https://arxiv.org/abs/cond-mat/9805204)
STUDY MATERIALS IN CB_23_24_PACK_10-
Find in the PACK the papers referred to in the discussion and pdf files of the lectures on clustering that were used in the CB course of 2021.
-
-
LECTURES N. 28, 29 and 30
Relevance of Bayes’ theorem in the analysis of sequences
(HA 10.2, bayesian model (parameter) selection: pseudo counts
generative probabilistic models
Markov order 0 models (urn models)
A bayesian classifier of disordered proteins ( a critique of, look at the priors (Bulashevska2008)
Entropy rules from Baldi and Brunak)
Bayes Factors in model selection: the relevance of priors (see HA eq. 10.5 and box 10.1)
STUDY MATERIALS AND SUGGESTIONS FOR PERSONAL STUDY IN CB-23_24_PACK_11-
Find here the slides that were used to introduce the discussion and materials for personal study
-
-
LECTURES N. 33, 34, 35 and 36
Prior and posterior probabilities (key formula10.3), pseudocounts (key formula 10.11)
Hidden Markov Models(HMM): basic structure (HA 10.3, see also Chap3_Durbin_Biological_Sequence_Analysis)
HMM Problems:Evaluation, Decoding, Learning (see slides: Introduction_Hidden_Markov_Models.pdf)
Decoding problem: the Viterbi algorithm (HA box 10.2) Training supervised/unsupervised of a HMM on a gapless profile associated to a protein family: Viterbi (minimum action path) vs Baum-Welsch (path integral) method (HA 10.3.3).
Forward/Backwards algorithms.-
Slides of the lectures on the structure and training of Hidden Markov Models
-
-
LECTURES N. 31 and 32
Introduction to Systems Biology
The chemical Master Equation
The Gillespie Algorithm
SEE THE SLIDES OF THE LECTURES IN CB_23_24_PACK_13
-
-
Here is the set of slides prepared and presented by the attending students
-