Section outline
-
Docente: Arch. Jessica Romor
Dottore di Ricerca, Università Sapienza di Roma, Dip. di Storia, disegno e restauro dell'architettura
E-mail: jessica.romor@uniroma1.it
Il disegno è il mezzo principale con il quale il progettista si esprime. Attraverso il disegno egli comunica determinate caratteristiche dell’oggetto rappresentato, selezionandole tra le infinite possibili, attraverso un processo di astrazione che dalla realtà, attraverso la capacità sintetica della mente, porta al disegno. Un disegno che per essere concepito e capito da chi lo legge presuppone la conoscenza e l’uso di: un linguaggio condiviso e determinato da regole precise attraverso il quale esprimere i pensieri; un lessico appropriato, costituito dalle forme proprie dell’architettura; una sintassi che consenta di porre in relazione le varie forme per comporle in strutture via via più complesse.
Ciò che consente poi di rendere concreti i pensieri del progettista sono gli strumenti che egli ha adisposizione: il disegno a mano e quello automatico o, per meglio dire, automatizzato. Il primo, dalla storia secolare, prevede l’utilizzo degli strumenti tradizionali e consente una rappresentazione rapida ed istantanea del pensiero: è il mezzo con il quale il progettista può confrontarsi con i colleghi, le maestranze o la committenza per ragionare sulle fasi di ideazione del progetto o sulle modifiche da apportare in corso d’opera, e rimane dunque uno strumento importantissimo per l’immediatezza dei risultati. Il disegno automatizzato, di più recente sviluppo e diffusione, è poi un altro strumento oggi indispensabile al progettista, che necessita di strumenti che contribuiscano ad aumentarne competitività e produttività, ottimizzando i tempi di creazione e gestione del progetto.
Obiettivo di questo corso è dunque quello di educare lo studente ad appropriarsi di una forma di comunicazione grafica e tecnica condivisa che consenta di esprimere e comunicare le caratteristiche peculiari di un progetto sia attraverso il disegno tradizionale, sia tramite quello automatizzato. La prima parte del corso sarà dedicata alla formazione del linguaggio dello studente, che apprenderà i metodi di rappresentazione, per via grafica e digitale, quali la doppia proiezione ortogonale, l’assonometria e la prospettiva. Parallelamente, lo studente imparerà a riconoscere e gestire le forme che costituiscono l’architettura, partendo dagli enti fondamentali quali il punto, la retta e il piano, e le relazioni che sussistono fra essi consentendo di giungere a forme più complesse (relazioni di simmetria, modularità, proporzionalità, rapporto pieno/vuoto, variazioni di scala, accentuazione della verticalità/orizzontalità, etc.). Durante il corso lo studente porterà avanti un tema architettonico specifico, che dovrà prima rappresentare e analizzare, per poi lavorare sull’espressione delle caratteristiche che il soggetto, inteso nella sua sintesi compositiva, presenta, attraverso la produzione di elaborati grafici e digitali che ne esaltino le proprietà.
-
Cosa significa “rappresentare l’architettura”: il ruolo del disegno nella professione dell’architetto (realtà > pensiero > disegno). Contenuti della rappresentazione: cosa descrivo, come lo descrivo, quali qualità scelgo di rappresentare, cosa voglio comunicare: ruolo dei metodi di rappresentazione nella comunicazione.
Obiettivi del corso:
1) appropriarsi del linguaggio (conoscere e utilizzare i metodi di rappresentazione e le convenzioni grafiche);
2) appropriarsi del lessico (riconoscere e utilizzare le forme proprie dell’architettura);
3) appropriarsi della sintassi (riconoscere le relazioni tra le forme, la genesi geometrica delle forme complesse).
Cenni sull’evoluzione del disegno digitale.
Introduzione all’esercitazione per l’apprendimento dei metodi: composizione di un modello fisico costituito da elementi semplici (scatole di cartone, rotoli di carata, oggetti di forma conica i piramidale, etc.; tasselli del domino; mattoncini lego; giochi froebeliani).
N.B. Compito per la lezione successiva: scegliere una serie di oggetti semplici (come quelli proposti a lezione), da comporre nella lezione successiva.
-
Cosa significa rappresentare: l’operazione di proiezione e sezione; il centro di proiezione, il quadro, il soggetto da rappresentare. Gli enti dello spazio euclideo e l'ampliamento dello spazio proiettivo: punto, retta, piano, direzione, giacitura. Cenni alla nomenclatura.
I metodi di rappresentazione. La prospettiva come metodo più generale di rappresentazione. L’assonometria come caso particolare di prospettiva: il centro di proiezione improprio, la direzione di proiezione; relazione tra direzione di proiezione, quadro e oggetto. Le proiezioni ortogonali come caso particolare di assonometria: la rappresentazione in pianta e alzato.
N.B. Per la lezione successiva preparare una composizione con gli oggetti raccolti, fotografarla ed eseguirne uno schizzo sul quale annotare le misure necessarie a rappresentarla nelle successive lezioni.
-
Prima lezione sulla rappresentazione in pianta e alzato. Si sono illustrati i principi della rappresentazione in doppia proiezione ortogonale, introducendo i concetti di piani e direzioni di proiezione in relazione alla rappresentazione del punto, della retta e del piano. Sono stati poi trattati gli enti in posizione particolare, il cui utilizzo è fondamentale nella soluzione dei principali problemi di rappresentazione in pianta e alzato: piani proiettanti in prima proiezione (e piani frontali come caso particolare), piani proiettanti in seconda (e piani orizzontali come caso particolare), piani di profilo.
Sono stati affrontati in seguito alcuni problemi di rappresentazione, quali: retta intersezione di un piano generico con un piano frontale; retta intersezione di un piano generico con un piano orizzontale; punto intersezione di una retta con un piano.
Al termine della lezione è stato presentato un modello che illustra le procedure per la rappresentazione in pianta e alzato del modello che gli studenti devono proporre per la prima esercitazione.
-
Seconda e ultima lezione sulla rappresentazione in pianta e alzato. Si sono affrontati alcuni problemi specifici relativi a:
- Rappresentazione del cerchio in pianta e alzato, nei due casi in cui il cerchio appartenga ad un piano proiettante in prima o appartenga ad un piano inclinato
- Rappresentazione di una figura generica appartenente ad un piano proiettante
In entrambi i casi proposti, si è trattato il tema del ribaltamento sul primo piano di proiezione del piano che contiene la figura sul quale ricostruire la vera forma della figura stessa e, in virtù dell’affinità che si viene a creare tra la figura ribaltata e la sua proiezione, al fine di individuare le proiezioni dei punti in prima e, in seguito, seconda proiezione.
-
Esempio di rappresentazione in pianta e alzato del modello della prima esercitazione. Nella dispensa sono illustrati i principali passaggi che caratterizzano la rappresentazione in pianta e alzato di un modello esemplificativo della prima esercitazione.
-
Le tavole, in formato A3 o A4, possono essere impaginate in orizzontale o verticale, come nell'esempio. In ogni caso, scelto un orientamento, è bene mantenerlo per tutte le altre tavole, siano essere realizzate a mano o in digitale, indipendentemente dall'orientamento del contenuto interno alla tavola.
-
Questo primo compito prevede la consegna di due tavole sulla rappresentazione in pianta e alzato del modello realizzato.
In particolare le due tavole devono contenere:
- tav. 01, fotografia/e del modello e schizzo del rilievo
- tav. 02, rappresentazione in pianta e alzato del modello
Dato che si tratta di tavole realizzate a mano, per essere consegnate on-line devono essere digitalizzate. Fatene dunque delle scansioni a 300 dpi a colori e salvatele in ".pdf" o ".jpg".
La consegna va effettuata entro le 23:55 di lunedì 20 ottobre p.v.
-
Introduzione alla rappresentazione digitale. Rappresentazione di geometrie e rappresentazione di oggetti. Rappresentazione matematica e numerica.
Che cos’è il Building Information Modeling: ruolo del BIM nella progettazione e nella gestione dell’edificio.
Contenuti del B.I.Model: volumi, materiali, abachi, etc.
Approccio al modello: sue rappresentazioni, piani di costruzione, scala, etc.
-
Introduzione alla rappresentazione del modello in ambito BIM sulla base della composizione di volumi trattata nelle precedenti lezioni.
Presentazione del modello, progetto delle operazioni di modellazione. Disegno dei profili nello spazio e relative estrusioni per la creazione dei solidi.
La rappresentazione del terreno.
Orientamento e illuminazione.
Controllo delle viste: piante, prospetti, sezioni, spaccati assonometrici.
Agli studenti è stato assegnato il compito di realizzare il modello digitale della composizione precedentemente realizzata da ognuno di loro per l'esercitazione sulla rappresentazione in pianta e alzato.
-
Indicazioni per la rappresentazione digitale della composizione astratta presentata nelle precedenti lezioni. A breve seguiranno ulteriori indicazioni per la modellazione di altri solidi particolari diversi da quelli presenti nel modello.
-
Cartiglio in formato A4 da utilizzare per la consegna delle tavole create con Revit. Per utilizzarlo, va caricato nel progetto così come indicato nella dispensa sulla stampa (richiamandolo cioè accedendo al percorso "menù vista/composizione tavole/tavola" e caricandolo cliccando su "carica...").
-
Se non riuscite ad utilizzare il cartiglio che ho creato, per incompatibilità con le versioni di Revit utilizzate (purtroppo non è previsto il salvataggio di progetti o famiglie nelle versioni precedenti!), potete modificare quello del quale disponete nel vostro progetto. In questa dispensa troverete le indicazioni necessarie per farlo.
-
Questa seconda consegna riguarda la rappresentazione digitale in pianta e alzato del modello della composizione astratta realizzata per la prima esercitazione.
La consegna consiste nella realizzazione di una tavola in formato A4 o A3 nella quale vanno impaginati la pianta e l'alzato del modello digitale realizzato, ad una scala opportunamente scelta in relazione alla dimensione del modello stesso (1:100, 1:200, 1:250, 1:300, ...).
-
-
Inserimento di riferimenti esterni (immagini) all'interno del modello.
Creazione dei volumi principali. Creazione di pareti e solai dai volumi precedentemente creati. Modifica di pareti e solai. Scelta del tipo di componenti e relativa modifica.
Inserimento di porte e finestre. Creazione di fori nelle pareti.
-
I collegamenti verticali: le scale.
La costruzione dei tetti a falde per via digitale.
La rappresentazione del modello: creazione di viste in proiezione ortogonale; scala di dettaglio.
Rappresentazione del terreno da curve di livello importate da file CAD.
Impaginazione e stampa.
-
L’assonometria con il metodo grafico: principi proiettivi; centro di proiezione e piano di proiezione. Modelli assonometrici: assonometria ortogonale e assonometria obliqua.
Nel dettaglio: l’assonometria ortogonale. Impostazione degli assi, rappresentazione del triangolo delle tracce (teorema di Schlömilch) e misura delle unità assonometriche.
Rappresentazione della composizione di solidi realizzata nelle precedenti lezioni in assonometria ortogonale isometrica per via grafica.
-
Costruzione dell'assonometria ortogonale isometrica della composizione di volumi realizzata nelle precedenti lezioni. Il disegno è presente sia in versione Rhinoceros, sia in versione Autocad.
-
Lezione 10 – L’assonometria per via grafica (parte II): assonometria obliqua. L’assonometria digitale.
Seconda e ultima lezione sulla rappresentazione assonometrica per via grafica.
Nel dettaglio: l’assonometria obliqua. Scelta degli assi e delle unità assonometriche (teorema di Polke), determinazione della direzione di proiezione. Illustrazione di casi particolari di assonometria obliqua: assonometria militare, assonometria cavaliera, assonometria speciale.
Rappresentazione della composizione di solidi realizzata nelle precedenti lezioni in assonometria obliqua militare per via grafica.
L'assonometria digitale.
-
Costruzione dell'assonometria obliqua militare della composizione di volumi realizzata nelle precedenti lezioni. Il disegno è presente sia in versione Rhinoceros, sia in versione Autocad.
-
Questa consegna prevede la realizzazione di due tavole in formato A4 o A3 contenenti rappresentazioni assonometriche del modello solido realizzato per la prima esercitazione.
Tavola 1 - Assonometria ortogonale isometrica.
- Scegliere la scala in funzione della dimensione del modello e della tavola sulla quale si lavora, in modo che il disegno riempia adeguatamente lo spazio. Potete lavorare in scala naturale (1:1),
oppure riducendo il modello (1:2, 1:3, ...) o ingrandendolo (2:1, 3:1, ...).
- Nel disegno va rappresentato il riferimento alla proiezione della terna di assi e delle relative unità assonometriche (come nel disegno Cad esemplificativo presente sul sito).Tavola 2 - Assonometria obliqua militare
- Per quanto riguarda scala e riferimento agli assi e alle unità, vale quanto detto per la prima tavola.- Le unità assonometriche sugli assi x' e y' vanno rappresentate in vera forma, mentre quelle sull'asse z' vanno scorciate (potete utilizzare un fattore di scala di 0.75, per esempio, come abbiamo fatto a lezione).
- L'orientamento dell'asse z' deve essere verticale, mentre gli assi x' e y' (tra loro perpendicolari nell'assonometria militare) si possono, per praticità, disegnare inclinati di 30°/60° rispetto al bordo
orizzontale del foglio (se si usa la squadretta 30°-60°-90°) o a 45° (se si utilizza invece la squadretta 45°-45°-90°).Per quanto riguarda l'impaginazione e l'inserimento delle varie informazioni, valgono le indicazioni della prima consegna.
-
Creare una tavola, analogamente a quanto fatto per la rappresentazione in pianta e alzato digitali, del modello realizzato per la prima esercitazione. Scegliere una vista assonometrica del modello digitale, impostare una scala adeguata, e impaginare in una tavola di formato A4 o A3.
Per le impostazioni grafiche della vista, adottare le medesime scelte per le viste in pianta e alzato.
-
Introduzione alla genesi delle curve e delle superfici.
Curve e superfici luogo geometrico. Approfondimento sulle superfici impiegate in architettura: archi e volte. Costruzione di profili costituiti da curve luogo geometrico: cerchio, ovali, curve policentriche.
Costruzione dell'ovale a tre centri.
Gli studenti dovranno realizzare una tavola disegnando a mano o con Autoicad le seguenti policentriche utilizzate come profili di archi, come nell'immagine al link sottostante:
- ovale a tre centri
- ovale a tre centri a rapporto fisso
- arco a sesto acuto equilatero
- arco a sesto tedesco
- arco a sesto acuto a influsso
-
Questa tavola, che può essere realizzata in formato A4 o A3, deve contenere i disegni, realizzati a mano o per via digitale con AutoCad (o in entrami i modi, per chi volesse cimentarsi in entrambe le tecniche!), delle seguenti curve policentriche impiegate in architettura come profili di archi:
- ovale a tre centri
- ovale a tre centri a rapporto fisso
- arco a sesto acuto equilatero
- arco a sesto tedesco
- arco a sesto acuto a influsso
Le procedure per la costruzione di queste curve sono riportate nella presentazione della lezione e sul testo Geometria descrittiva - volume II alle pagine indicate nella bibliografia specifica della lezione.
-
Rappresentazione digitale di superfici luogo geometrico: volte semplici e composte.
Costruzione con Revit delle seguenti volte semplici:
- vola a botte con profilo a tutto sesto
- volta a botte con profilo a sesto acuto
- volta a vela
- volta ad anello
Costruzione con Revit delle seguenti volte composte:
- volta a crociera
- volta a padiglione su impianto quadrato
- volta a padiglione su impianto rettangolare
-
La consegna prevede la realizzazione di due tavole in formato A4 che contengano rispettivamente i passaggi che caratterizzano la costruzione della volta a vela e della volta a crociera con Revit, come rappresentate a lezione.
I vari passaggi possono essere rappresentati con delle catture da schermo, utilizzando il tasto "stamp" della tastiera o una applicazione come lo "strumento di cattura" di Windows, e poi composti in Photoshop o software simile. Le tavole devono sempre riportare i soliti dati relativi al corso, allo studente e all'argomento trattato nella tavola.
-
Esempio di impostazione di analisi grafica e rappresentazione di un'architettura nota tramite software BIM (Revit).
Individuazione, prima in pianta e poi in alzato, dei rapporti proporzionali (1:1, 2:3, 3:4, rapporto aureo, ...), del modulo che regola la composizione, delle relazioni geometriche tra le parti (simmetria, rotazione, traslazione, variazione di scala, etc.).
Presentazione dei temi di architettura riguardanti la seconda esercitazione da assegnare agli studenti.
-
Creazione di schemi distributivi, abachi, impaginazione degli elaborati.
Per una sitografia degli argomenti suddetti, fare rifermento ai link contenuti nella lezione 8 del corso Building Information Modeling 2013 disponibile sul sito e-learning della Sapienza.
-
Procedura per la prenotazione del tema:
- formate i gruppi, da 2 o 3 persone (chi avesse l'esigenza di lavorare da solo, me lo comunichi via e-mail e concorderemo una soluzione alternativa);
- scegliete il tema. E' necessario che solo UNO DEI COMPONENTI del gruppo effettui la prenotazione, comunicandomi in seguito via e-mail la composizione del gruppo stesso. Chi decidesse di lavorare in tre, è pregato di non considerare i temi riservati a chi lavora in coppia.NB - E' possibile effettuare la scelta da oggi, 28 novembre, a martedì 6 gennaio p.v.
-
La lezione sarà tenuta dal Prof. Graziano Mario Valenti, Professore Associato all'Università Sapienza di Roma, Facoltà di Architettura, docente dei corsi di Scienza della rappresentazione II e Fondamenti e applicazioni della geometria descrittiva.
-
- Introduzione al metodo della rappresentazione prospettica: l'operazione di proiezione e sezione da un centro proprio.
- La prospettiva per la rappresentazione della realtà e i suoi riferimenti spaziali: il punto di vista, il piano di quadro, il piano geometrale sul quale poggia il soggetto che osserva, il piano dell'orizzonte, l'orizzonte, il punto principale, la distanza principale, il cerchio di distanza.
- Rappresentare la retta: traccia di una retta (punto in cui la retta oggettiva incontra il quadro), e fuga di una retta (immagine - cioè rappresentazione sul quadro - della direzione della retta oggettiva).
- Rappresentare il piano: traccia (retta di intersezione tra il piano oggettivo e il quadro) e fuga del piano (immagine - cioè rappresentazione sul quadro - della giacitura del piano).
- Condizioni di appartenenza retta-piano: una retta e un piano si appartengono quando si appartengono anche le relative tracce e fughe.
- Condizioni di parallelismo: due rette parallele hanno in comune la direzione e quindi hanno anche in comune l'immagine della loro direzione sul quadro, cioè il punto di fuga; due piani paralleli hanno in comune la giacitura e quindi hanno anche in comune l'immagine della loro giacitura sul quadro, cioè la retta di fuga.
- Proprietà di rette in posizione particolare: rette parallele al quadro hanno le immagini tra loro parallele; rette verticali hanno come immagini rette verticali; rette orizzontali hanno come immagini rette verticali; rette perpendicolari al quadro hanno fuga nel punto principale.
- Proprietà di piani in posizione particolare: piani paralleli al quadro hanno le immagini tra loro parallele; piani verticali hanno traccia e fuga verticali; piani orizzontali hanno traccia e fuga verticali; piani perpendicolari al quadro hanno la fuga che passa per il punto principale.
-
- Introduzione alla misura in prospettiva: solo gli enti che appartengono al quadro sono in vera forma, mentre segmenti e angoli che non vi appartengono appaiono scorciati.
- Misura dell'angolo formato da due rette: ribaltamento sul quadro delle rette proiettanti la direzione delle rette date e misura dell'angolo da esse formato in vera forma sul quadro.
- Misura di rette
- Illustrazione del concetto delle rette di misura, in grado di staccare sulla retta data e sulla traccia del piano che la contiene segmenti uguali. Concetto di punti di misura e cerchio di misura.
- Algoritmo per la misura di una retta:
- Definizione della retta da misurare (traccia e fuga devono essere rappresentate)
- Scelta del piano che appartiene alla retta sul quale condurre le operazioni di misura
- Individuazione della coppia di punti di misura in relazione alla retta e al piano scelto (tramite ribaltamento; applicazione della regola secondo la quale: "il punto di misura dista dal punto di fuga della retta da misurare quanto questo dista dal punto di vista".)
- Determinazione sulla traccia del piano del segmento da misurare in vera misura
- Proiezione del segmento riportato in vera misura sulla traccia sulla retta in prospettiva tramite rette di misura.
- Misura di rette in posizione particolare
- Rette perpendicolari al quadro - Le rette perpendicolari al quadro hanno i punti di misura sul cerchio di distanza.
- Rette parallele al quadro - Hanno come punto di misura uno qualsiasi dei punti che appartengono alla fuga del piano che le contiene.
-
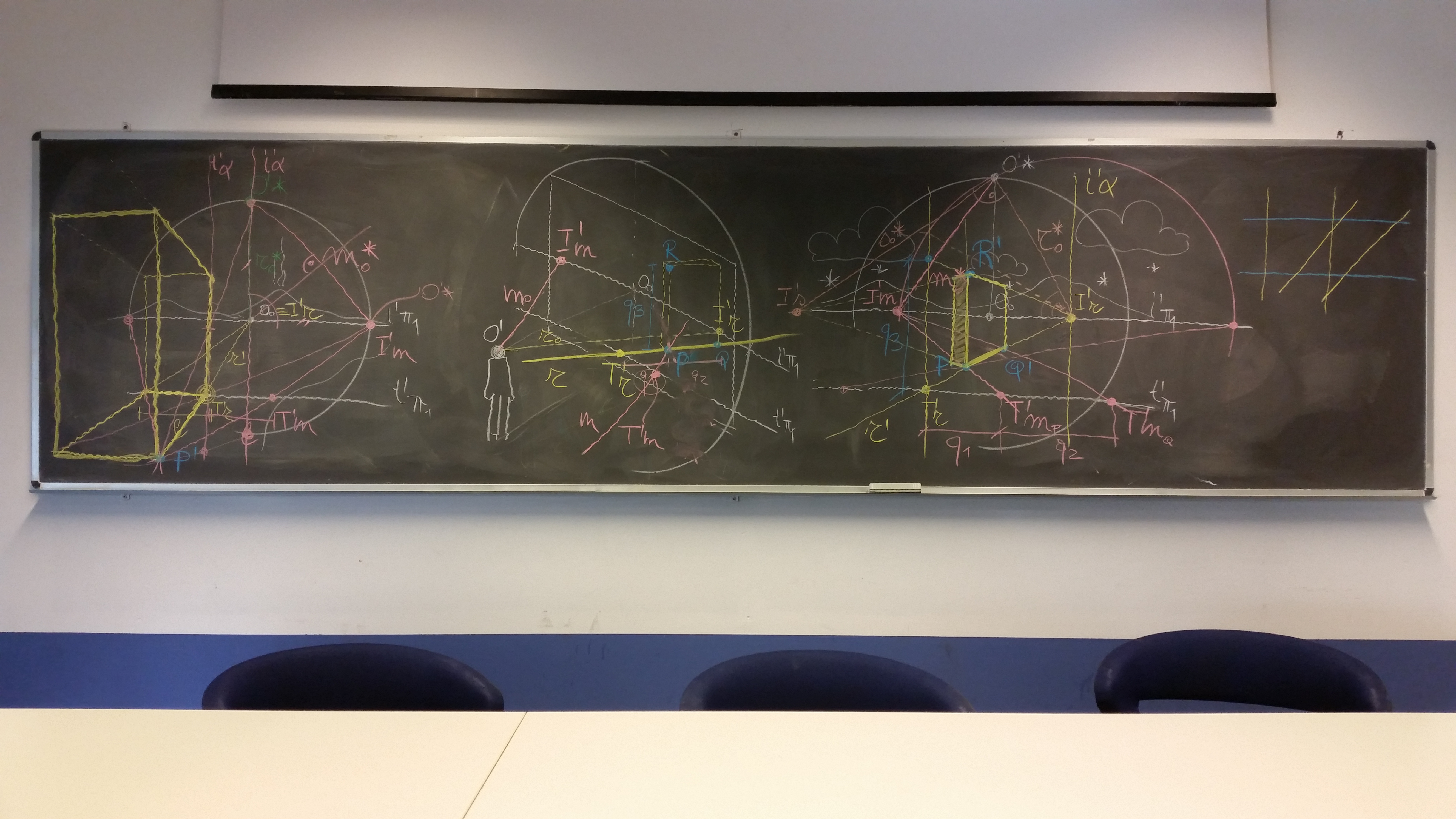
Lezione dedicata alla rappresentazione prospettica del modello realizzato per la prima esercitazione, semplificato togliendo gli elementi inclinati.
-
Questa consegna prevede la realizzazione di una prospettiva per via grafica della composizione astratta realizzata per la prima esercitazione.
Per eseguire tale prospettiva, seguite le indicazioni della dispensa che ho inserito in questa stessa sezione, dedicata alla lezione 17.
Vi ricordo, come già detto a lezione che:
- il disegno va realizzato a mano su foglio A4 o A3;
- dovete togliere dalla composizione il solido inclinato, se ne avete uno;
- date alla composizione una dimensione confrontabile a quella dell'architettura, come se essa fosse il modello in scala di un edificio (come avete fatto per la costruzione del modello in Revit);
- scegliete una scala di rappresentazione che vi servirà per iniziare il disegno: tutto ciò che appartiene al quadro apparirà in vera forma sul quadro, scalato secondo il rapporto di riduzione che avete scelto. Ricordate che la distanza tra orizzonte e traccia del geometrale esprime l'altezza dell'osservatore (circa 170 cm), quindi se state facendo una prospettiva in scala 1:50 la distanza tra orizzonte e traccia del geometrale sarà, in scala sul foglio, 3.4 cm.
Per qualsiasi dubbio, fate riferimento alla dispensa suddetta.
-
Lezione dedicata ad esercizi sulla rappresentazione prospettica, relativi in particolare alla misura di angoli e rette orizzontali e verticali.
-